Web 动画基础所需知识点
介绍
动画里的涉及到角度与坐标的关系,主要通过数学三角学知识来处理。而在物理渲染中,模型的处理主要通过物理学的公式来实现。
下面涉及到的数学公式和物理公式可以参考这两篇《常用的数学公式》和《常用的物理公式》来理解。
canvas 里的坐标系
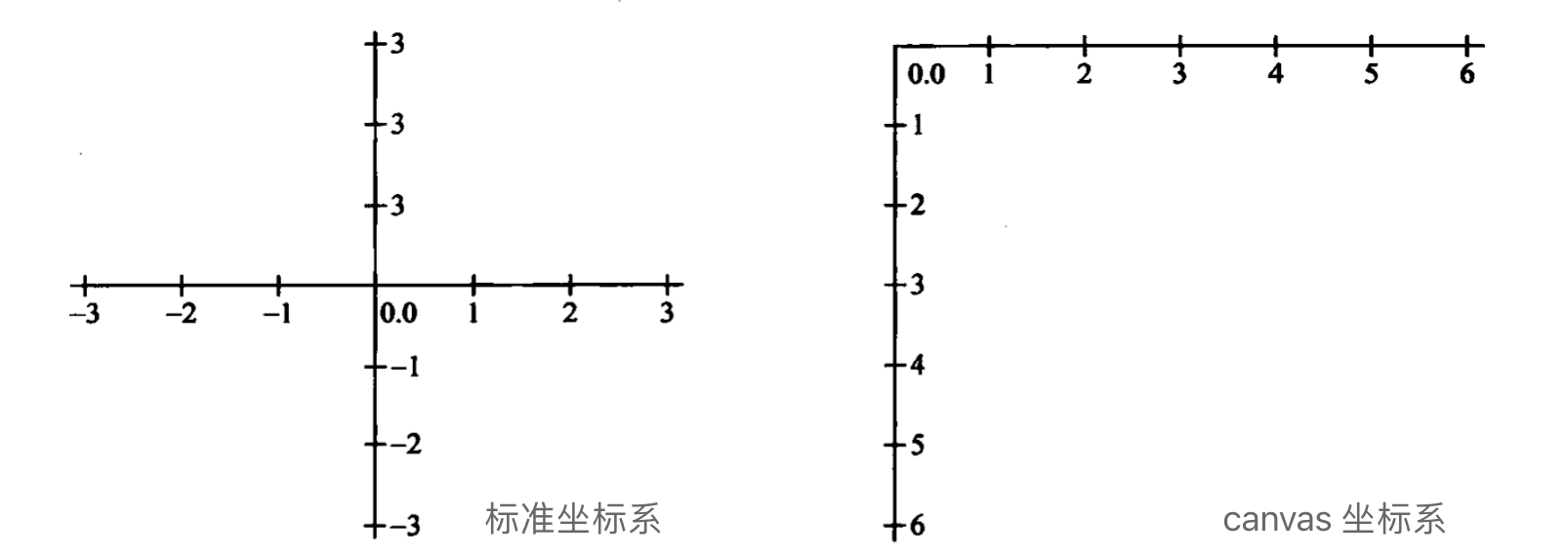
canvas 里的坐标系中心并不是在画布的正中心,而是在画布的左上角。
这个坐标系有它的历史背景,因为电子枪是从左往右,从上往下扫描屏幕的,后来也成为了图形学编程里屏幕坐标系的习惯,这种习惯也方便了图形编程中某些问题的处理。
canvas 四象限的角度
在 canvas 里角度的正负表示 如下:
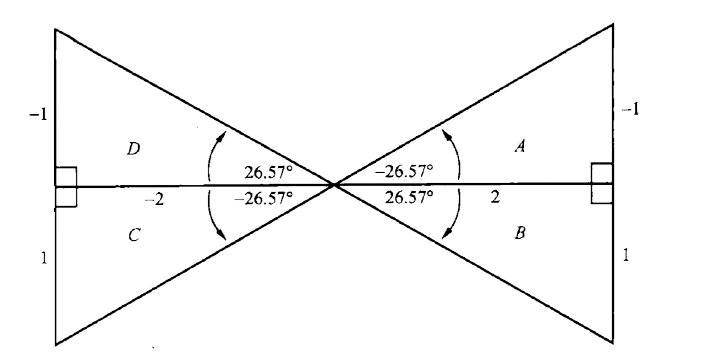
通常,我们可以通过 Javascript 的反正切函数 Math.atan2(y,x) 来获取对应的角度,这里的角度单位是弧度。
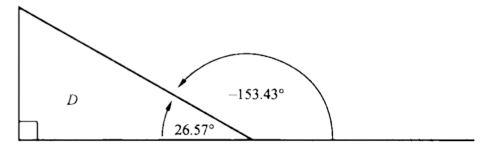
在 canvas 坐标系统里的角度计算:
Math.atan2(-1, -2) * 180 / Math.PI
// => -153.43494882292202
当我们要逆时针计算角度时,要减去角度大小。而顺时针计算时,要加上角度大小。如果是两个角度向量,那么直接使用向量加法即可,图形编程中可以使用弧度来表示角度向量。
角速度
在 canvas 里下面的方向的速度分解到 $x$ 轴 $y$ 轴的向量表示如下:
在知道了角度 (angle)和速度 (speed)之后,我们利用三角函数可以获取 $vx$, $vy$的速度向量:
vx = Math.cos(angle) * speed
vy = Math.sin(angle) * speed
这里的 angle 是弧度,我们可以通过转换公式来转换角度:
vx = Math.cos(degree * Math.PI / 180) * speed
vy = Math.sin(degree * Math.PI / 180) * speed
角加速度
加速度和速度向量类似,由大小 (力的大小) 和方向组成,由此可以分解到 $x$ 轴和 $y$ 轴上:
let force = 8
let angle = 450
let ax = Math.cos(angle * Math.PI / 180) * force
let ay = Math.sin(angle * Math.PI / 180) * force
把加速度向量加入速度向量中:
vx += ax;
vy += ay;
把速度向量加入坐标中:
object.x += vx;
object.y += vy;
坐标旋转

1. 只知道半径 (radius) 和旋转后的角度 (angle) 的情况
通过下面的公式来计算旋转后的坐标:
object.x = centerX + cos(angle) * radius
object.y = centerY + sin(angle) * radius
2. 只知道旋转 (rotation) 角度和起始坐标 (x,y) 的情况
通过下面的公式来计算旋转后的坐标:
x1 = x * cos(rotation) - y * sin(rotation)
y1 = y * cos(rotation) + x * sin(rotation)
在数学线性代数中,上面旋转变换可以表示变换矩阵:$ R(\theta) = \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} $,其中 $\theta$ 是旋转角度,通常以弧度为单位。
如果对一个坐标 $(x,y)$ 进行旋转变换运算,可以写成向量方程形式的线性方程组:
$ \begin{bmatrix}\cos(\theta) \\ -\sin(\theta)\end{bmatrix}x + \begin{bmatrix}\sin(\theta) \\ \cos(\theta)\end{bmatrix}y = \begin{bmatrix}rx \\ ry\end{bmatrix} $。(rx,ry) 是旋转后的坐标。
我们可以编写一个旋转变换矩阵的函数来实现坐标的旋转:
const point = [1,2]
const rotation = Math.atan2(point[1], pointp[0]) * 180 / Math.PI; // 弧度
const cos = Math.cos(rotation);
const sin = Math.sin(rotation);
const rotationMatrix = [
[cos, -sin],
[sin, cos]
];
function rotate(point: number[], matrix: number[][]) {
const rotatedX = matrix[0][0] * point[0] + matrix[0][1] * point[1]
const rotatedY = matrix[1][0] * point[0] + matrix[1][1] * point[1]
return [rotatedX, rotatedY]
}
// 举例
const [rx, ry] = rotate(point, rotationMatrix); // 顺时针旋转后的坐标
逆向旋转也有下面的逆向旋转变换矩阵:
const cos = Math.cos(rotation);
const sin = Math.sin(rotation);
const inverseRotationMatrix = [
[cos, -sin],
[sin, cos]
];
// 举例
const [rx, ry] = rotate(point, inverseRotationMatrix); // 逆时针旋转后的坐标
如果是相对坐标 (centerX, centerY) 为旋转中心,可以把公式写成下面这样:
x1 = (x - centerX) * cos(rotation) - (y - centerY) * sin(rotation) + centerX
y1 = (y - centerY) * cos(rotation) + (x - centerX) * sin(rotation) + centerY
逆向旋转可以用下面的公式:
x1 = (x - centerX) * cos(rotation) + (y - centerY) * sin(rotation) + centerX
y1 = (y - centerY) * cos(rotation) - (x - centerX) * sin(rotation) + centerX
这种高级坐标旋转在于你可以在不知道旋转中心的坐标(centerX,centerY)的情况下,提前得出公式,则你可以很方便的动态改变旋转中心。
Q&A:上面是如何推导出来的呢?
1.首先通过起始点(x,y)和目标点(x1,y1)的半径和角度,我们可以知道以下等式:
x = radius * cos(angle)
y = radius * sin(angle)
x1 = radius * cos(angle + rotation)
y1 = radius * sin(angle + rotation)
2.接下来利用下面数学的三角恒等式:
// 余弦和角公式
cos(a + b) = cos(a) * cos(b) - sin(a) * sin(b)
// 正弦和角公式
sin(a + b) = sin(a) * cos(b) + cos(a) * sin(b)
3.我们把1里的 x1、y1 公式利用三角恒等式展开:
x1 = radius * cos(angle) * cos(rotation) - radius * sin(angle) * sin(rotation)
y1 = radius * sin(angle) * cos(rotation) + radius * cos(angle) * sin(rotation)
4.最后把1里的 x、y 变量代入公式,就得到下面的方程:
x1 = x * cos(rotation) - y * sin(rotation)
y1 = y * cos(rotation) + x * sin(rotation)
碰撞检测
两物体碰撞
这里两个矩形相交就返回 true,否则 false。通常复杂的图形会使用矩形或圆形作为碰撞区,来作为碰撞检测。
function checkCollision(rectA, rectB) {
return !(
rectA.x + rectA.width < rectB.x ||
rectB.x + rectB.wdith < rectA.x ||
rectA.y + rectA.height < rectB.y ||
rectB.y + rectB.height < rectA.y
)
}
对于近似矩形的对象,可以采用上面的方法。
物体与点碰撞
function checkCollision(rectA, x, y) {
return !(
x < rect.x || x > rect.x + rect.width ||
y < rect.y || y > rect.y + rect.height
)
}
对于不规则的图形,如果要求高精度,可以基于物体与点的碰撞检测,来定制一个方案。
水平矩形与圆形的碰撞检测
这里有种方案可以精确的检测圆形和矩形的碰撞。
它的解决思路是找出矩形距离圆形在 x 轴和 y 轴最近边界点 (testX, testY),然后基于距离去做碰撞检测,下面的图枚举了全部圆形位置,更容易去理解:
我们可以得到下面的碰撞检测代码:
function rectangleCircleCollision(rect, circle) {
const cx = circle.x
const cy = circle.y
const radius = circle.radius
const rx = rect.x
const ry = rect.y
const rw = rect.width
const rh = rect.height
// temporary variables to set edges for testing
let testX = cx
let testY = cy
// which edge is closest?
if (cx < rx) testX = rx // test left edge
else if (cx > rx + rw) testX = rx + rw // right edge
if (cy < ry) testY = ry // top edge
else if (cy > ry + rh) testY = ry + rh // bottom edge
// get distance from closest edges
const distX = cx - testX
const distY = cy - testY
const distance = Math.sqrt(distX * distX + distY * distY)
// if the distance is less than the radius, collision!
if (distance <= radius) {
console.log('hited')
return true
}
console.log('not hit')
return false
}
斜面反弹
在处理墙面反弹的时候,通常我们只需使 x 轴或 y 轴的速度向量取反即可,但是在斜面上却并不能这么处理。
我们要做的是:旋转整个系统使反弹面水平,然后做反弹,最后再旋转回来。这意味着反弹面、物体的坐标位置和速度向量都旋转了。
假设:
- 小球 (ball) 的位置为 (x, y) ,速度为 (vx, vy) 。
- 反弹面 (line) 的倾斜角度为 rotation,反弹面的位置为 (lineX, lineY) 。
1.那么通常小球的动画代码会是下面这样:
ball.vx = vx
ball.vy = vy
ball.x += ball.vx
ball.y += ball.vy
2.在上面我们已经知道了如何做坐标旋转,所以我们可以获取旋转后小球的水平位置及速度:
let cos = Math.cos(line.rotation)
let sin = Math.sin(line.rotation)
// 小球相对于斜面的位置
let x1 = ball.x - line.x
let y1 = ball.y - line.y
// 旋转后,小球水平位置的坐标
let x2 = x1 * cos + y1 * sin
let y2 = y1 * cos - x1 * sin
// 旋转后,小球水平位置的速度
let vx1 = ball.vx * cos + ball.vy * sin
let vy1 = ball.vy * cos - ball.vx * sin
上面的旋转使用了三角恒等式的差角公式,即减去旋转角度来达到水平角度的 $0°$
注意 x1, y1 的后续计算都将是相对于斜面的坐标的相对位置。在计算完最后,小球的位置是需要回到原有的坐标系中的,即绝对位置。
3.执行反弹时,这里需要把小球的位置置于平面上,防止小球出现嵌入斜面的情况。
虽然现实中,这样计算时有误差,但是从动画效果上来看,并无大碍:
if(y2 > -ball.radius) {
y2 = -ball.radius
}
4.最后一步是把旋转到水平位置后的小球坐标和速度旋转回去:
// 小球相对斜面的坐标反转计算
x1 = x2 * cos - y2 * sin
y1 = y2 * cos + x2 * sin
// 小球相对斜面的速度反转计算
ball.vx = vx1 * cos - vy1 * sin
ball.vy = vy1 * cos + vx1 * sin
// 小球相对坐标系的反转计算,得到它的绝对位置
ball.x = line.x + x1
ball.y = line.y + y1
单轴的动量守恒
使用动量守恒原理,可以确定两个物体碰撞后的反应。因此你可以说:“碰撞前,一个物体以速度 A 运动,另一个物体以速度 B 运动;碰撞后,一个物体速度变成了 C,另一个物体的速度变成了 D”。
动量守恒公式:${\displaystyle m_{1}v_{01}+m_{2}v_{02}=m_{1}v_{1}+m_{2}v_{2}}$
动能守恒公式:$\frac{1}{2}m_1v_{01}^2 + \frac{1}{2}m_2v_{02}^2 = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2$
对上面的动量守恒公式和动能守恒公式,利用数学中的代入消元法,可以得到两个未知数的公式:
$$ \displaystyle v_1 = \frac{ (m_1 - m_2) \times v_{01} + 2\times m_2 \times v_{02} } {m_1 + m_2} = \left({\frac {m_{1}-m_{2}}{m_{1}+m_{2}}}\right)v_{01}+\left({\frac {2m_{2}}{m_{1}+m_{2}}}\right)v_{02} $$
$$ \displaystyle v_2 = \frac{ (m_2 - m_1) \times v_{02} + 2\times m_1 \times v_{01} } {m_1 + m_2} =\left({\frac {m_{2}-m_{1}}{m_{1}+m_{2}}}\right)v_{02}+\left({\frac {2m_{1}}{m_{1}+m_{2}}}\right)v_{01} $$
通过以上两个公式,我们可以在提前知道两个物体的速度和质量的情况下,计算出碰撞后各自在单轴上的速度。
动画上,通常尺寸越大的物体质量也越大,你可以体现这种关系,依据小球的尺寸大小来设置它们的质量。通常情况下,我们会不断尝试调整质量的值,直到动画看起来感觉比较好。
优化
在当计算出一个物体的最终速度后,可以根据未碰撞前两个物体的相对速度来计算出另一个物体的最终速度。
这里需要的知识点是:碰撞前后,他们的总速度 (相对速度) 是相等的。
总速度等式为:$\large v_{total} = v_{01} - v_{02} = v_{2} - v_{1}$
因此可以优化上面两个求最终速度的公式:
$$ \displaystyle v_1 = \frac{ (m_1 - m_2) \times v_{01} + 2\times m_2 \times v_{02} } {m_1 + m_2} = \left({\frac {m_{1}-m_{2}}{m_{1}+m_{2}}}\right)v_{01}+\left({\frac {2m_{2}}{m_{1}+m_{2}}}\right)v_{02} $$
$\displaystyle v_2 = (v_{01} - v_{02}) + v_1$
双轴上的动量守恒
上面的一维碰撞,你可以通过一个冗长的公式获取碰撞后两物体的速度,这几乎可以即插即用,现在再加入另一维度。
原理和策略
我们需要计算两个小球位置形成的角度,并逆时针旋转整个场景 (位置和速度) ,这和上面的斜面反弹做得是一样的事。
实现
1.给定两个球 ball0 和 ball1,质量为 mass,速度为 vx。所以正常情况他们的动画代码如下:
ball0.x += ball0.vx
ball0.y += ball0.vy
ball1.x += ball1.vx
ball1.y += ball1.vy
2.根据三角学知识,可以用 Math.atan2(dy,dx) 来计算角度,我们计算正弦和余弦并把它们保存下,因为它们将会反复用到:
let dx = ball1.x - ball0.x
let dy = ball1.y - ball0.y
let angle = Math.atan2(dy,dx)
let sin = Math.sin(angle)
let cos = Math.cos(angle)
然后,要对两个小球的速度和位置进行坐标旋转。
旋转后的位置是 x0、y0、x1、y1,旋转后的速度是 vx0、vy0、vx1、vy1。我们把 ball0 作为中心点,所以它的坐标为 (0,0) 。
因为坐标旋转后它也不变,所以可以这么写:
// ball0 旋转后的位置
let x0 = 0
let y0 = 0
3.旋转后的位置和速度:
// ball1 旋转后的位置
let x1 = dx * cos + dy * sin
let y1 = dy * cos - dx * sin
// ball0 旋转后的速度
let vx0 = ball0.vx * cos + ball0.vy * sin
let vy0 = ball0.vy * cos - ball0.vx * sin
// ball1 旋转后的速度
let vx1 = ball1.vx * cos + ball1.vy * sin
let vy1 = ball1.vy * cos - ball1.vx * sin
4.根据动量守恒公式,现在使用 vx0、ball0.mass、ball1.mass 执行一维碰撞反应:
let vxTotal = vx0 - vx1
vx0 = ((ball0.mass - ball1.mass) * vx0 + 2 * ball1.mass * vx1) / (ball0.mass + ball1.mass)
vx1 = vxTotal + vx0
x0 += vx0
x1 += vx1
上面我们就获取了碰撞后,ball0 和 ball1 在 x 轴上的速度了,我们把新的 x 速度加在了原来的 x 位置上。
5.最后,我们把一切都旋转回来:
// 位置旋转回来
let x0Final = x0 * cos - y0 * sin
let y0Final = y0 * cos + x0 * sin
let x1Final = x1 * cos - y1 * sin
let y1Final = y1 * cos + x1 * sin
// 获得最终的绝对坐标
ball1.x = ball0.x + x1Final
ball1.y = ball0.y + y1Final
ball0.x = ball0.x + x0Final
ball0.y = ball0.y + y0Final
// 把速度旋转回来
ball0.vx = vx0 * cos - vy0 * sin
ball0.vy = vy0 * cos + vx0 * sin
ball1.vx = vx1 * cos - vy1 * sin
ball1.vy = vy1 * cos + vx1 * sin
到此,我们的球体在二维碰撞反应就完成了。