Tower_of_Hanoi.jpeg

游戏简介

初始状态：有三根柱子 A，B，C 。 A 柱上有 N 个 (N > 1) 穿孔圆盘，盘的尺寸由下到上依次变小。

游戏目标：把所有 A 柱的圆盘全部移到 C 柱，并保持原有顺序。

游戏规则：

  1. 每次只能移动一个圆盘；
  2. 无论在哪个柱上，移动时大盘必须都在小盘下面。

算法目标：求完成游戏目标的最少步骤。

这里有个模拟汉诺塔的可视化工具：tower of hanoi。

问题分析

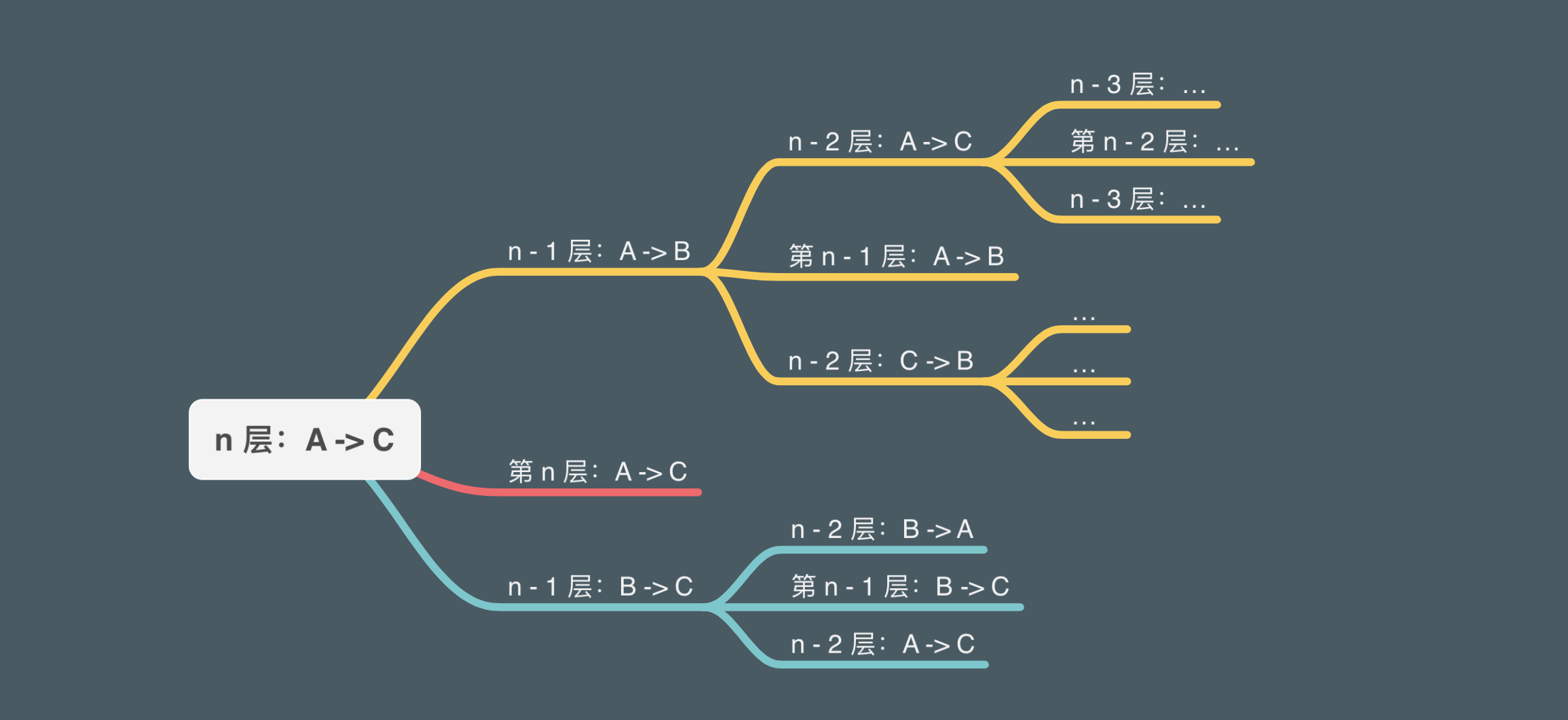
汉诺塔问题是递归的经典用例，我们可以把这个大问题拆解为重复的小问题，每个人小问题重复几个步骤。解决了一个小问题，就解决了下个小问题必要条件。

对于3层圆盘情况下，我们把上面的2层圆盘当做整体来操作。

对于4层圆盘情况下，我们把上面的3层圆盘当整体来操作：

如果我们固定4层圆盘最底层的圆盘，其实就是在解决层数为3的汉诺塔问题。并且每一个小问题，都是三个步骤。

所以当我们有 n 层圆盘时，我们要解决的问题是层数为 n-1 的子问题，以此继续类推：

hanoi.png

算法实现

通过上面的分析，我可以通过递归分成三个步骤编写我们的代码：

const A = ' A 柱'
const B = ' B 柱'
const C = ' C 柱'

function move(orderNumber, from, to) {
  console.log(`把第 ${orderNumber} 层圆盘，从${from}移至${to}`)
}

function hanoi(n, from, to, helper) {
  if (n > 0) {
    // 第一步
    hanoi(n - 1, from, helper, to)
    // 第二步
    move(n, from, to)
    // 第三步
    hanoi(n - 1, helper, to, from)
  }
}

hanoi(4, A, C, B)

值得注意的是每个子问题唯一要做的事，就是寻找目标柱子和辅助柱子。

上面的算法我们得到了以下输出结果：

把第 1 层圆盘，从 A 柱移至 B 柱
把第 2 层圆盘，从 A 柱移至 C 柱
把第 1 层圆盘，从 B 柱移至 C 柱
把第 3 层圆盘，从 A 柱移至 B 柱
把第 1 层圆盘，从 C 柱移至 A 柱
把第 2 层圆盘，从 C 柱移至 B 柱
把第 1 层圆盘，从 A 柱移至 B 柱
把第 4 层圆盘，从 A 柱移至 C 柱
把第 1 层圆盘，从 B 柱移至 C 柱
把第 2 层圆盘，从 B 柱移至 A 柱
把第 1 层圆盘，从 C 柱移至 A 柱
把第 3 层圆盘，从 B 柱移至 C 柱
把第 1 层圆盘，从 A 柱移至 B 柱
把第 2 层圆盘，从 A 柱移至 C 柱
把第 1 层圆盘，从 B 柱移至 C 柱

参考资料：

> https://www.youtube.com/watch?v=1QgJEcnsqsQ&ab_channel=李永乐老师

> https://en.wikipedia.org/wiki/Tower_of_Hanoi#Solution